[Research] Recurrent Neural Network (RNN)

1. Introduction

As we all know, forward neural networks (FNN) have no connection between neurons in the same layer or in cross layers. The propagation direction is single. Though it is easier to learn but to some extent, it reduces the power of neural networks.
In FNN, the output only relies on the current input. However, in practice, the output is associated not only with the input of current epoch but past few epochs. Like, video, speech, text, those signals are hard to be handled by FNN.
Recurrent neural network (RNN) is one kind of NN that neurons can receive information from themselves and other neurons which forms a circuit. This model is more coherent to the neural structure of beings. RNN has been widely used in speech recognition, language models and natural language generation. So in this post, we are going dissect this model.

Neural networks, whether recurrent or feedforward, can receive as input raw sensor signals. However, applying them to features derived from the raw sensor signals often leads to higher performance. Discovering adequate features requires expert knowledge, which necessarily limits a systematic exploration of the feature space. Convolutional networks (CNNs) have been suggested to address this.

2. Background

2.1 Independent variables vs. Dependent variables

Before talking about RNN, we need to have an overview of the relationship between random variables. This relationship includes the independent form and the dependent form.  

The independent variable is the variable whose change isn’t affected by any other variable in the experiment. In contrast, dependent variables describe what changes as a result of the changes of other dependent variables.  As for multi independent variables, they are parallel. But they constitute a graphical structure for multi dependent variables, which is also called the probabilistic graphical model.

probabilistic graphical model

2.2 Probabilistic Graphical Model (PGM)

PGM is a probabilistic model which uses graphs to represent the relationship of dependent variables. A node in the graph can represent one or a group of variables. The side between two nodes shows the probabilistic relationship. 

PGM can be divided into two classifications: undirected graph and directed graph. The directed graph is also called Bayesian Network (The Hidden Markov Model is the simplest dynamic Bayesian Model). The undirected graph is also called Markov Network.  

2.3 Hidden Markov Model

In this model, the variables can be divided into two groups: status variables or hidden variables and observable variables. 

Status variables or hidden variables cannot be observable. It can be used to give feedback to outside depending on different inputs. 

observable variables are measurable that give clues to infer the status of a system.

3. Simple RNN model

3.1 Time Delay Neural Network (TDNN)

TDNN is a NN that add a time delay in non-output layers of feedforward neural network (FNN) to record a few recent outputs of a certain neuron. For example, X is a neuron in the input layer. Xt means the value that X sends to a neuron in the next layer at time eepoch t. So, Xt-1, Xt-2, ... Xt-p+1 means the recent p input of X. Then the function of this so-called time delay is to record those outputs {Xt, Xt-1, Xt-2, ... Xt-p+1} and generate a new input to the neuron in the next layer.  That means, at epoch t, the neurons in l+1 layer are related to the recent p outputs of neurons in l layer.

Figure 3.1

If we consider the origin input as an image. The recent p inputs are like p pixels in a window. TDNN is like a simple convolutional neural network (CNN).

3.2 Nonlinear Autoregressive with Exogenous Inputs Model，NARX

Autoregressive Model (AR) is a model that is used to process temporal series, whose function is to predict the status of a variable depending on past status. It is employed to predict itself.

Figure 3.2

where, yt is the prediction of y at t epoch. w0 is a constant parameter and ε is the random noise (subject to normal distribution). w is the weight for each past status. 

Nonlinear Autoregressive with Exogenous Inputs Model is a model that combines time delay NN and AR but it is nonlinear.

 

Figure 3.3

From the equation in figure 3.3, we can see that yt is related to recent p input x and output y.

f(·) means nonlinear function.

3.3 Simple Recurrent Network, SRN

For section 3.2, we apply it to neural networks, we can get a kind of classic neural network, recurrent neural network (RNN).

Given an input series X(1:T)=(X1.....XT). So the status of neurons in next hidden layer ht is expressed in the form:

Figure 3.4

h0=0. so we can give a RNN model like: (including input layer, hidden layer and output layer, each layer only has one neuron.)

Figure 3.5

According to feedforward neural network model with three layers, let zt stand the pure input of hidden layer. f(·) means the non-linear activation function, e.g. logistic, tanh and ReLU. W is the status-status (transformation) weight matrix, U is the input-status weight matrix, b is the bias. ht is the status at t. And yt means the output at t. V is the status-output weight matrix. Then we have:

Figure 3.6

So now we have a basic neural network unit for RNN. At each time epoch, the model will get an input. At the same time, the status will be transformed along the time. Since the main feature of RNN is the status transformation, it is not necessary to give an output at each epoch. So the output y is optional. 
If we combine multi basic RNN models at different epochs and expanse in the order of time, we have: 

Figure 3.7

Figure 3.7-2

So this is a simple RNN model with three layers: the input layer, the hidden layer and the output layer. Each layer has T neurons.

3.4 Stacked Recurrent Neural Network，SRNN 

The power of neural networks relies on the depth of networks. More hidden layers, stronger learning ability neural networks are. 

Based on section 3.3, we increase the depth of hidden layers, then we have:

Figure 3.8

So the status equation turns:

Figure 3.9

From the figure 3.8 and 3.9, we can see the link weight between 2 layers at the same epoch is the input-status matrix, U; the link weight between 2 status in the same layer is the status-status matrix, W; Each hidden layer neuron has a bias, b. The so-called sharing weights are those parameters in the same color are same. 
This is how to stack multi hidden layers for RNN models. Until now, what I show you is the RNN with a very simple structure whose feature is T input, T status in each hidden layer and T output. Actually, RNN can be adapted to different structures to apply to different problems. 

4. Three different modalities of RNN

RNN can be applied to many different forms of machine learning tasks. There are mainly three modalities of RNN:  Sequence to Classification model, Synchronous Sequence to Sequence (Seq2Seq) model and asynchronous Sequence to Sequence model (also called Encoder-Decoder).

4.1 Sequence to Classification model (Seq2C)

Seq2C is mainly used to classify sequential data. The input is a sequence and the output is classification. For instance, in text classification, the input is sequential words and the output is the classification of this text.
Assume an input X(1:T)=(X1.....XT). The length is T. The output y is {1, ..., C}. We can input this X at different time epoch, like {X1, X2, X3, ..., XT) into RNN. The status we can get is {h1, h2, h3, ..., hT}. Instead of giving an output at each epoch, we only give one output for classification. 
Here we have 2 forms. One form is to take the hT as the final feature and give it to a classifier. The other is take the mean of the whole status as the final feature and send it to a classifier.

Figure 4.1

4.2 Synchronous Sequence to Sequence

Synchronous Sequence to Sequence model is mainly used for sequence labeling. That is to say, there is an output at each epoch which I showed you in section 3.3. 

Figure 4.2

4.3 Asynchronous Sequence to Sequence (Encoder-Decoder)

Asynchronous Sequence to Sequence is also called Encoder-Decoder model which has been used widely. This model doesn't require the strict reflection relationship between the input sequence and the output sequence as well as the same length. For instance, the input is word sequence, the output is the word sequence of a target language.
Similarly, we assume the input X is X(1:T)=(X1.....XT). The output is Y(1:M)=(y1, ..., yM). The process is realized by encoding and then decoding as shown in the figure below:

Figure 4.3

Figure 4.4 Encoder-Decoder model example

5. Parameters learning of RNN

Basically, the parameters of RNN also learn via gradient descent.
Under supervised learning, given an training example, (x,y): X(1:T)=(X1.....XT); Y(1:T)=(y1, ..., yT). That is to say, at each epoch, there is an output yt. Then the loss function (e.g. cross entropy and mean square error) at epoch t is:

Figure 5.1

As I said in a post about gradient descent and random gradinet descent, we often use batch
gradient descent to train parameters. So the loss function is the sum of loss functions of a batch of examples. So,

Figure 5.2

The inside of RNN has a recurrent structure, so the learning style is a little different from the way of feedforward neural networks. There are two ways to compute the gradient: Backpropagation through time (BPTT); Real-time recurrent learning (RTRL).

5.2 The number of parameters

From Figure 3.6, we can see all parameters we have are U, W, b and V(optional). So If we only consider parameters in the hidden layers, U, W and b are included.

The input is current xt and previous state ht-1. The dimension of x and h keep unchanged. If the size of x is m and h is n. The sum of parameters (U,W,b) is (m+n)*n+n.  

Thus, the status-status weight is a n*n matrix. 

The input-status weight is a m*n matrix.

The bias is 1*n.

When use matrix, the relationship can be expressed in the form:

Figure 5.2-1

5.2 Backpropagation through time (BPTT)

The feature of BPTT is that the loss function at epoch t only propagates back to the parameters before t epoch (inclusive). Like shown below, the yellow arrow only relates the parameters at t-2 as well as before t-2. And the blue arrow and the red arrow all follow this rule.  

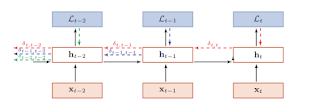Figure 5.3 BPTT

Considering Figure 3.6, we have:

Figure 5.4

Here an important feature of RNN is that the basic RNN model shares all parameters (including U, W and b) after expansion along time. For Stacked Recurrent Neural Networks (shown in Figure 3.8), the parameters in the same layer are same and in different layers are different. Here is an example:

Figure 5.5

Then we need to compute the partial derivation of the sum loss function subject to the parameters. Combining the matrix in figure 5.2-1, we have:

Figure 5.6

Here, i and j stand the row and column of the matrix W, respectively. [hk-1]j is the jth component of the status at k-1 epoch. IIi(x) is the short for the vector [0,0,...[hk-1]j,...,0]T
Because there is a recursive relationship between statuses. We assume δ(t,k) means the derivative of the loss at t epoch subject to the pure input zk at k epoch, then:

Figure 5.7

Figure 5.8

Therefore, in order to compute the gradient, we need a whole feedforward computation and back computation to update the parameters.

5.3 Real-time recurrent learning (RTRL)

The purpose of RTRL is to give an output at each epoch. If at t+1, we give an output and get a loss function. Then we compute the derivative of the current loss function:

Figure 5.9

Unlike BPTT, RTRL computes the gradient via feedforward style. 
Comparison:
BPTT and RTRL are all based on gradient descent, feedforward model and back model apply chain rules to compute gradient. In RNN, the dimension of output is far smaller than the dimension of inputs. Thus, the computation load of BTPP is low but it needs to store intermediate gradients at all epochs which increase the space complexity. RTRL does not need feedback of gradients. Therefore, it is very suitable for online learning or infinite sequence learning.

6. Gated RNN

 RNN face two problems, gradient exploding problem and gradient vanishing problem as shown below. In theory, RNN can build the relationship between current status and all past statuses. However, when the time interval is longer enough, RNN will appear these two problems leading to RNN only can learn short-term relationship. The model determines the long dependencies of RNN. This is so-called Long-Term Dependencies Problem.  

Figure 6.1

In order to solve this problem, Researchers invented the Gated RNN.

6.1 Long short-term memory, LSTM

LSTM is the most successful RNN model that has been widely applied in many areas, e.g. speech recognition, machine interpretation, voice model and text generation. LSTM mitigates the long-term dependencies problem via linear connections. Linear connections and gated control are very effective to avoid the gradient vanishing problem. In fact, this mechanism also can be applied to deep feedforward neural networks. 

In essence, adding linear connections for variables is more close to the way things happen. We know that things are always related to each other. Considering a more complex relationship can recover more potential relations which are not easy to understand. Graph is a good model to establish more connections between things. So it is easy to say that RNN is kind of a graph network. The graph network is a emerging research direction which is not mature. 

Then, let's have a look at the structure inside of LSTM.
From figure 6.2, we can see apart from the input and status, some other variables are included.    

Figure 6.2

Three kinds of gates:

• forget gate: ft, control how much information should the inner status at last epoch, ct-1, forget.
• input gate: it, control how much information should the candidate inner status c't save.
• output gate: ot control how much information should the real inner status ct send out to outer status ht. 

When ft =0, it=1, memory unit will be cleared out. ct=c't.
When ft =1, it=0, memory unit will copy the previous content. ct=ct-1.

Let's look at the structure of a LSTM recurrent unit. we can see all input (including observations and outer status at last epoch) will be sent to three gates and the inner status, respectively. Then the activation function determines how these gates and inner status work (sounds like natural selection).

Figure 6.3 LSTM recurrent unit

Figure 6.4 

6.2 Gated Recurrent Unit，GRU

                                                                                                                                                                          https://keras.io/                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   

Reference

推导过程：
https://zhuanlan.zhihu.com/p/27901936
https://zhuanlan.zhihu.com/p/38816145

https://nndl.github.io/chap-%E5%BE%AA%E7%8E%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C.pdf

Smartphone-based Activity Recognition and Multi-sensor Fusion based Indoor Positioning System

IoT2US Lab won 3^rd place in the premier competition of the 10^th International Conference on Indoor Positioning and Indoor Navigation (IPIN). There are fifteen teams in all from top universities (e.g. Ghent University), institutes or high tech companies (e.g. Intel, Tencent, LINE) and indoor positioning professional companies (e.g. Xihe Tech, Fineway, AraraDS) all over the world. This is one of the most world-famous two indoor positioning competitions, IPIN and Microsoft Indoor Localization Competition (IPSN) [2].

Team information

The work is a product of IoT2US Lab, in the School of (EECS), QMUL, in collaboration with UCL, Electronic Engineering department. Our team members are Bang Wu (QMUL), Chengqi Ma (UCL), Stefan Poslad (supervisor, QMUL), David Selviah (supervisor, UCL), Wei Wu (WHU), Xiaoshuai Zhang (QMUL) , Guangyuan Zhang (QMUL) , Zixiang Ma (QMUL).

Competition Goal

The goal of this competition track is to evaluate the performance of different indoor localization solutions based on the signals available to a smartphone (such as WiFi readings, inertial measurements, etc…) and received while a person is walking along several regular unmodified multi-floor buildings. This track is done off-site, so all data for calibration and evaluation is provided by competition organizers before the celebration of the IPIN conference. The competition teams can calibrate their algorithmic models with several databases containing readings from sensors typically found in modern mobile phones and some ground-truth positions. Finally, each team will compete using additional database files, but in this case, the ground-truth reference is not given and must be estimated by the competitors. This is an off-line competition where all competitors have the same data of the testing environment, so custom on-site calibration is not allowed.

Our Solution: Smartphone-based Activity Recognition and Multi-sensor Fusion based  Indoor Positioning System

Performance

Poster Display

Distance algorithms (Similarity Measurement) in Machine Learning

1. Euclidean Distance

2. Manhattan Distance

3.Chebyshev Distance

4.Minkowski Distance

5.Standardized Euclidean distance

6.Mahalanobis Distance

7. Cosine

8. Hamming distance

9. Jaccard similarity coefficient

10. Correlation coefficient 

11. Correlation distance

12. Information Entropy

Reference:

https://blog.csdn.net/hit_kongquan/article/details/6278768

[Research] Particle Filter

1. Introduction

A stochastic model is a tool for estimating probability distributions of potential outcomes by allowing for random variation in one or more inputs over time. Stochastic models include the Gauss distribution based stochastic model and non-Gauss distribution based stochastic model. According to the stochastic model, Filters can be divided into two classes: 1) Bayes filter, particle filter with non-Gauss distribution based stochastic model; 2) Kalman filter, extended Kalman filter and Unscented Kalman filter with Gauss distribution based stochastic model.

Figure 1: classes of filters

Actually, when dealing with uncertain situations, we usually set the Gauss model as its stochastic model. However, that is not suitable for any situations. Thus, Bayes filter and particle filter are designed for cases using non-Gauss model. In the last post, I introduced Bayes filter, in this post, I will focus on the particle filter. In the beginning, I will give you an overview of particle filters.  And then details will be given.

Figure 2. Bayes filter framework

Figure 3. Overview of the particle filter

2. Inference Model

Particle filter and Bayes filter share the same inference model. Because in the Bayes filter, the posterior probability is hard to compute. We usually use Monte Carlo sampling method to approximate this posterior probability. That is the main idea of the particle filter. Instead of directly computing the posterior probability, the particle filter is to generate many random variables (called particles) to approaching this probability to conduct filtering.

From figure 2, the framework of Bayes filter, we know in a dynamic system (u means the activation to keep the system dynamic), x means the state variables and z the measurement variables. At each time epoch, the last state can be transited into the next state using Bayes Theorem based on existing information, which is the so-called prediction. When there is a measurement at current epoch, it will be fused to compute the posterior, which is the so-called update.

However, there are some conditions for Bayes inference. 1) the system will be dynamic which is already met. 2) The transition of the system states should be followed first-order Markov chain. It means the current state is only determined by the last state. For example, p(xt|x1,x2,...,xt-1) = p(xt|xt-1). 3) variables of measurements are independent to each other. p(zt|z1,z2,...,zt-1) = p(zt).

Bayes filter uses a recursive form to approach the optimal solution of the posterior probability density function (filtering). The optimal estimation of the system state is implemented by using the posterior probability density function, generally like, Maximum a posterior estimate (MAP) and minimum mean square error (MMSE). 

Figure 4. Estimation models

However, as for nonlinear and non-Guass system, it is hard to get the complete solution of the posterior probability. Thus, we usually use approximation methods to approach integration. the particle filter is a method to use the Monte Carlo sampling method to approximate this posterior probability.  

3. Importance Sampling (IS)

In section 2, we talked about the principle of the particle filter is to use the Monte Carlo method to generate particles to approximate the posterior probability. The process is: assume we can extract a few samples meeting p(xt|yt) and they are independent and identically distributed, x_t^(i), i = 1,...,N, then the expectation estimation of an arbitrary function f(xt) can be approached by using the form of sum.

Figure 5. sum to approaching integration

Then we can sum up three steps of Monte Carlo sampling:

1. Build a probability model
2. Generate Sampling from the appointed probability model
3. Compute some estimators of these samples 

Then there is a question, generally, we don't know the information about this posterior probability, how can we generate particles to approximate it? That is what we call importance sampling.

The process of importance sampling is to arbitrarily import a known and easy-to-sample importance probability density function q(xt|z(1:t)). Then we generate N samples from this probability and use their weighted sum to approximate the posterior probability. Then we have

Figure 6. the Importance Sampling

That is the main idea of the Importance Sampling. However, here are two problems. 

• How to distribute the weights?
• At each epoch, we need to use all measurements to generate new samples and weights. It is very low-efficiency.    

Then a sequential importance sampling method is proposed to solve these problems.

4. Sequential Importance Sampling (SIS)

Sequential important sampling is the basis of the particle filter, which is based on the sequential analysis in statistics. It is applied to Monte Carlo to estimate the posterior probability recursively. The process is:

Assume the importance probability density function is q(x0:t|z1:t), then we have:

Figure 7. the sequential Importance Sampling probability density function

According to first-order Markov chain, current state is only determined by last one, and each measurement is independent from each other.

Figure 8. Applied Markov feature 

So then we need to get the sequential posterior probability density function. 

Figure 9. the sequential posterior probability density function.

And then we get the sequential weights:

Figure 10. the sequential weights.

From figure 7, 9, 10, we get the sequential model of importance sampling function, posterior model function and weights. Among them, the importance sampling function is user-defined, the posterior model can be computed by known probability, and so does the weights. With all variables known, we just need to intialize the weights and importance function. Particle filter will be implemented recursively. 

Based on aforesaid content, i give the process of the particle filter

Figure 11. particle filter process.

5. Weight Degeneracy

To get the correct state estimation, we hope the variance of weights is close to zero. However, sequential Monte Carlo faces the problem of weight degeneracy, which makes the variance of weights greater. And the meaning of weight degeneracy is after a few iterations, only a small number of them have greater weights and the others' weights are approximately zero. It leads to a decrease in efficient particles. The performance of particle filter degrades.

Generally, we use the number of efficient particles, Neff,  to evaluate the degeneracy degree. The smaller of Neff, the severer of weight degeneracy.  

Figure 12. the evaluation of weight degeneracy.

We set a threshold Nthresh, if the Neff is greater than Nthresh, there means weight degeneracy. We need to launch resampling to mitigate it.

Facing this weight degeneracy, there are two methods to mitigate it. 1) resampling; 2) chose more suitable importance density function. 

6. Solution 1: Resampling 

To solve the weight degeneracy problem, many kinds of resampling methods are used for it. 1) systematic resampling; 2) residual resampling; 3) stratified resampling; 4) multinomial resampling. There is a paper making a comparison of those resampling schemes and displaying the details of this method. Here I explain the process of them use code. The main rule of resampling is to generate the sub indexes and use it to chose particles. 

6.1 systematic resampling

def systematic_resample(weights):
    """ Performs the systemic resampling algorithm used by particle filters.
    This algorithm separates the sample space into N divisions. A single random
    offset is used to to choose where to sample from for all divisions. This
    guarantees that every sample is exactly 1/N apart.
    Parameters
    ----------
    weights : list-like of float
        list of weights as floats
    Returns
    -------
    indexes : ndarray of ints
        array of indexes into the weights defining the resample. i.e. the
        index of the zeroth resample is indexes[0], etc.
    """
    N = len(weights)
    # make N subdivisions, and choose positions with a consistent random offset
    positions = (random() + np.arange(N)) / N
    indexes = np.zeros(N, 'i')
    cumulative_sum = np.cumsum(weights)
    i, j = 0, 0
    while i < N:
        if positions[i] < cumulative_sum[j]:
            indexes[i] = j
            i += 1
        else:
            j += 1
    return indexes

6.2 residual resampling

def residual_resample(weights):

    """ Performs the residual resampling algorithm used by particle filters.

    Based on observation that we don't need to use random numbers to select

    most of the weights. Take int(N*w^i) samples of each particle i, and then

    resample any remaining using a standard resampling algorithm [1]

    Parameters

    ----------

    weights : list-like of float

        list of weights as floats

    Returns

    -------

    indexes : ndarray of ints

        array of indexes into the weights defining the resample. i.e. the

        index of the zeroth resample is indexes[0], etc.

    References

    ----------

    .. [1] J. S. Liu and R. Chen. Sequential Monte Carlo methods for dynamic

       systems. Journal of the American Statistical Association,

       93(443):1032–1044, 1998.

    """

    N = len(weights)

    indexes = np.zeros(N, 'i')

    # take int(N*w) copies of each weight, which ensures particles with the

    # same weight are drawn uniformly

    num_copies = (np.floor(N*np.asarray(weights))).astype(int)

    k = 0

    for i in range(N):

        for _ in range(num_copies[i]): # make n copies

            indexes[k] = i

            k += 1

    # use multinormal resample on the residual to fill up the rest. This

    # maximizes the variance of the samples

    residual = weights - num_copies     # get fractional part

    residual /= sum(residual)           # normalize

    cumulative_sum = np.cumsum(residual)

    cumulative_sum[-1] = 1. # avoid round-off errors: ensures sum is exactly one

    indexes[k:N] = np.searchsorted(cumulative_sum, random(N-k))

    return indexesdef residual_resample(weights):

    N = len(weights)

    indexes = np.zeros(N, 'i')

    num_copies = (np.floor(N*np.asarray(weights))).astype(int)

    k = 0

    for i in range(N):

        for _ in range(num_copies[i]): # make n copies

            indexes[k] = i

            k += 1

    # use multinormal resample on the residual to fill up the rest. This

    # maximizes the variance of the samples

    residual = weights - num_copies     # get fractional part

    residual /= sum(residual)           # normalize

    cumulative_sum = np.cumsum(residual)

    cumulative_sum[-1] = 1. # avoid round-off errors: ensures sum is exactly one

    indexes[k:N] = np.searchsorted(cumulative_sum, random(N-k))

    return indexes

6.3 stratified resampling

def stratified_resample(weights):
    """ Performs the stratified resampling algorithm used by particle filters.
    This algorithms aims to make selections relatively uniformly across the
    particles. It divides the cumulative sum of the weights into N equal
    divisions, and then selects one particle randomly from each division. This
    guarantees that each sample is between 0 and 2/N apart.
    Parameters
    ----------
    weights : list-like of float
        list of weights as floats
    Returns
    -------
    indexes : ndarray of ints
        array of indexes into the weights defining the resample. i.e. the
        index of the zeroth resample is indexes[0], etc.
    """
    N = len(weights)
    # make N subdivisions, and chose a random position within each one
    positions = (random(N) + range(N)) / N
    indexes = np.zeros(N, 'i')
    cumulative_sum = np.cumsum(weights)
    i, j = 0, 0
    while i < N:
        if positions[i] < cumulative_sum[j]:
            indexes[i] = j
            i += 1
        else:
            j += 1
    return indexes

6.4 multinomial resampling

def multinomial_resample(weights):
    """ This is the naive form of roulette sampling where we compute the
    cumulative sum of the weights and then use binary search to select the
    resampled point based on a uniformly distributed random number. Run time
    is O(n log n). You do not want to use this algorithm in practice; for some
    reason it is popular in blogs and online courses so I included it for
    reference.
    
   Parameters
   ----------
    weights : list-like of float
        list of weights as floats
    Returns
    -------
    indexes : ndarray of ints
        array of indexes into the weights defining the resample. i.e. the
        index of the zeroth resample is indexes[0], etc.
    """
    cumulative_sum = np.cumsum(weights)
    cumulative_sum[-1] = 1.  # avoid round-off errors: ensures sum is exactly one
    return np.searchsorted(cumulative_sum, random(len(weights)))

6.5 comparison of these resampling methods

To test the performance of these methods, we set the weight list is a, and draw the figures of resampling using different methods. 

a = [.1, .2, .3, .4, .2, .3, .1]

np.random.seed(4)

plot_multinomial_resample(a)

plot_residual_resample(a)

plot_systematic_resample(a)

plot_stratified_resample(a)

Then I give the sampling performance of them:

Figure 13. comparison of four resampling methods

The performance of the multinomial resampling is quite bad. There is a very large weight that was not sampled at all. The largest weight only got one resample, yet the smallest weight was sample was sampled twice. Most tutorials on the net that I have read use multinomial resampling, and I am not sure why. Multinomial resampling is rarely used in the literature or for real problems. I recommend not using it unless you have a very good reason to do so.

The residual resampling algorithm does excellently at what it tries to do: ensure all the largest weights are resampled multiple times. It doesn't evenly distribute the samples across the particles - many reasonably large weights are not resampled at all.

Both systematic and stratified perform very well. Systematic sampling does an excellent job of ensuring we sample from all parts of the particle space while ensuring larger weights are proportionality resampled more often. Stratified resampling is not quite as uniform as systematic resampling, but it is a bit better at ensuring the higher weights get resampled more. In practice, both the stratified and systematic algorithms perform well and similarly across a variety of problems. 

7. Solution 2: choosing the importance density function

The choice of the importance probability density function is very important to the performance of the particle filter. The standard to choose a importance sampling function is to make the variance of particles minimum.

In applications, we usually choose the transition probability function of the state as the proposal (importance) probability, p(xt|xt-1). The weight is in the form:

Figure 14. take state transition probability as the proposal probability

The state transition probability has a simple form and is easy to implement. In situations with not high-accuracy measurement, it can achieve a good filtering performance. 

However, the state transition probability doesn't consider the latest measurement leading to a gap between samples and real posterior distribution. When the measurement model has high accuracy, this difference will be notable.

8. Practice

To let you be familiar with the particle filter. I found an example from filterpy.
filterpy is a open package which includes many kinds of filters, e.g. Bayes filter, particle filter, Kalman filter, extended Kalman filter and UKF.
from filterpy.monte_carlo import systematic_resample
from numpy.linalg import norm
from numpy.random import randn
import scipy.stats
import matplotlib.pyplot as plt
from numpy.random import uniform

def create_uniform_particles(x_range, y_range, hdg_range, N):
    particles = np.empty((N, 3))
    particles[:, 0] = uniform(x_range[0], x_range[1], size=N)
    particles[:, 1] = uniform(y_range[0], y_range[1], size=N)
    particles[:, 2] = uniform(hdg_range[0], hdg_range[1], size=N)
    particles[:, 2] %= 2 * np.pi
    return particles

def create_gaussian_particles(mean, std, N):
    particles = np.empty((N, 3))
    particles[:, 0] = mean[0] + (randn(N) * std[0])
    particles[:, 1] = mean[1] + (randn(N) * std[1])
    particles[:, 2] = mean[2] + (randn(N) * std[2])
    particles[:, 2] %= 2 * np.pi
    return particles

def predict(particles, u, std, dt=1.):
    """ move according to control input u (heading change, velocity)
    with noise Q (std heading change, std velocity)`"""

    N = len(particles)
    # update heading
    particles[:, 2] += u[0] + (randn(N) * std[0])
    particles[:, 2] %= 2 * np.pi

    # move in the (noisy) commanded direction
    dist = (u[1] * dt) + (randn(N) * std[1])
    particles[:, 0] += np.cos(particles[:, 2]) * dist
    particles[:, 1] += np.sin(particles[:, 2]) * dist

def estimate(particles, weights):
    """returns mean and variance of the weighted particles"""

    pos = particles[:, 0:2]
    mean = np.average(pos, weights=weights, axis=0)
    var  = np.average((pos - mean)**2, weights=weights, axis=0)
    return mean, var

def update(particles, weights, z, R, landmarks):
    for i, landmark in enumerate(landmarks):
        distance = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
        weights *= scipy.stats.norm(distance, R).pdf(z[i])

    weights += 1.e-300      # avoid round-off to zero
    weights /= sum(weights) # normalize

def neff(weights):
    return 1. / np.sum(np.square(weights))

def resample_from_index(particles, weights, indexes):
    particles[:] = particles[indexes]
    weights[:] = weights[indexes]
    weights.fill(1.0 / len(weights))

    
def run_pf1(N, iters=18, sensor_std_err=.1, 
            do_plot=True, plot_particles=False,
            xlim=(0, 20), ylim=(0, 20),
            initial_x=None):
    landmarks = np.array([[-1, 2], [5, 10], [12,14], [18,21]])
    NL = len(landmarks)
    
    plt.figure()
   
    # create particles and weights
    if initial_x is not None:
        particles = create_gaussian_particles(
            mean=initial_x, std=(5, 5, np.pi/4), N=N)
    else:
        particles = create_uniform_particles((0,20), (0,20), (0, 6.28), N)
    weights = np.ones(N) / N

    if plot_particles:
        alpha = .20
        if N > 5000:
            alpha *= np.sqrt(5000)/np.sqrt(N)           
        plt.scatter(particles[:, 0], particles[:, 1], 
                    alpha=alpha, color='g')
    
    xs = []
    robot_pos = np.array([0., 0.])
    for x in range(iters):
        robot_pos += (1, 1)

        # distance from robot to each landmark
        zs = (norm(landmarks - robot_pos, axis=1) + 
              (randn(NL) * sensor_std_err))

        # move diagonally forward to (x+1, x+1)
        predict(particles, u=(0.00, 1.414), std=(.2, .05))
        
        # incorporate measurements
        update(particles, weights, z=zs, R=sensor_std_err, 
               landmarks=landmarks)
        
        # resample if too few effective particles
        if neff(weights) < N/2:
            indexes = systematic_resample(weights)
            resample_from_index(particles, weights, indexes)
            assert np.allclose(weights, 1/N)
        mu, var = estimate(particles, weights)
        xs.append(mu)

        if plot_particles:
            plt.scatter(particles[:, 0], particles[:, 1], 
                        color='k', marker=',', s=1)
        p1 = plt.scatter(robot_pos[0], robot_pos[1], marker='+',
                         color='k', s=180, lw=3)
        p2 = plt.scatter(mu[0], mu[1], marker='s', color='r')
    
    xs = np.array(xs)
    #plt.plot(xs[:, 0], xs[:, 1])
    plt.legend([p1, p2], ['Actual', 'PF'], loc=4, numpoints=1)
    plt.xlim(*xlim)
    plt.ylim(*ylim)
    print('final position error, variance:\n\t', mu - np.array([iters, iters]), var)
    plt.show()

from numpy.random import seed
seed(2) 
run_pf1(N=5000, plot_particles=False)

The result is:

Figure 15. the result after particle filter 

Reference

https://nbviewer.jupyter.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/12-Particle-Filters.ipynb
https://wenku.baidu.com/view/88896d2b453610661ed9f4b4.html
https://blog.csdn.net/heyijia0327/article/details/40899819
https://www.bilibili.com/video/av32636259/?p=2
https://wenku.baidu.com/view/150db14ac850ad02de8041a9.html