[Research] The principle of Bayes Filter

The principle of Bayes Filter

1. Introduction

The Bayesian filter is an important class of filters. It is widely used in object tracking, robot positioning and so on. And it is the basis of filters like the Kalman Filter (KF), Extended Kalman Filter (EKF), Information Filter (IF) and Particle Filter (PF). It is a type of filter using prior knowledge and causal knowledge (also called likelihood) to deduce posterior knowledge. This process can be displayed by Bayes Theorem:

Equation 1. Bayes Theorem

Actually, there are two types of filters, parametric filters (e.g. Kalman filters, Information filters) and non-parametric filters (e.g. histogram filter, discrete Bayes Filter, Particle Filter).

• The feature of parametric filters is that the system status can be expressed by parametric models. That means the posterior information of the system is explicit. The most common parametric model is Gauss model (corresponding distribution is normal distribution). The parameters used are mean and variance.
• The feature of non-parametric filters is the system is independent to the posterior information. Unlike the parametric filters whose posterior information can be analytically displayed by models (e.g. Gauss model), non-parametric filters use finite samples to approximate posterior probability.   

As I said before, both parametric filters and non-parametric filters are using the framework of Bayes Theorem. Combine prior information (prediction model) and causal information (measurement model) to deduce the posterior information. So it is quite beneficial to have a good understanding of Bayes Filter. Therefore, this post will focus on the principle and some related background of the Bayes Filter. 

2. Background

2.1 Probability and Bayes Theorem

• P(X=xi) means the probability when X equals xi
• For discrete variables, P(⋅) is called the probability mass function. e.g. p(X) = {0.1, 0.2, 0.7}
• For continuous variables, P(x∈(a,b)) =∫p(x)dx is called the probability density function

Figure 2.1.1 the probability density function

• Joint Probability: p(X=x  and  Y=y)=p(x,y), is called the Joint Probability Density Distribution. If X and Y are independent, p(x,y)=p(x)p(y).
• Conditional Probability: p(X=x|Y=y)  means given Y=y, compute the probability when X=x. p(x|y)=p(x,y)/p(y); p(x,y)=p(x|y)p(y)=p(y|x)p(x). Specially, if X is independent to Y, p(x|y)=p(x).
• Law of total probability:

Equation 2. law of total probability

• Bayes Theorem: as shown in Equation 1 above. From it, we can see p(y) is independent to p(x|y). So p(y) can be viewed as a normalization factor of which function is to keep p(x|y) under 1.

Equation 3. normalization factor

2.2 Discrete-time Markov Chain

A discrete-time Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. This process can be displayed by: 

Equation 4. The feature of the probability of Discrete-time Markov Chain4

There are a few features of Markov Chain:

• memorylessness for first-order Markov Chain: From Equation 3, we know the current status is only dependent on the most previous status. 
• First-order and n-order: Generally, we talk about the first-order Markov Chain. But Markov chain also has a version for high-order. High-order MC is an extension of first-order MC. The form is like this:  we see compared to first-order MC, n-order MC is dependent on the n most previous state, which means n-order MC has a memory.

Equation 5. First-order and n-order of MC

• Transition probability: is the probability going from state i to state j in single-step transition or multi-step transition. e.g.

Equation 6. Transition probability

• Transition Matrix: If the state space is finite, the transition probability distribution can be represented by a matrix, called the transition matrix. Similarly, the transition matrix has a single-step transition, multi-step transition or mix. Here is an example of a single-step transition:

Equation 7. Transition matrix

• Connectivity: every two states are connected. some of them are directly connected and others are not directly connected where we can use transition matrix to connect them.
• Stationary distribution: given an arbitrary state Π = [π(1), π(2),..., π(j)], Σπ(j) = 1; if Π(i) = Π(j)Pij, we call it stationary distribution. The code showing below give you an example to validate this distribution. You will find that the state in stationary distribution is independent on the initial state. That means, only Pij will affect this stationary distribution. 

#python code

p=np.array([[0.65,0.28,0.07],[0.15,0.67,0.18],[0.12,0.36,0.52]])

p2 = np.array([[0.21,0.68,0.11]])

#p2 = np.array([[0.286, 0.489, 0.225]])

for i in range(20):

    print("index", i)

    p2 = np.dot(p2,p)

    print(p2)

index 0

[[0.2517 0.554  0.1943]]

index 1

[[0.270021 0.511604 0.218375]]

index 2

[[0.27845925 0.49699556 0.22454519]]

index 3

[[0.28249327 0.49179188 0.22571485]]

index 4

[[0.28447519 0.48985602 0.22566879]]

index 5

[[0.28546753 0.48909735 0.22543512]]

index 6

[[0.28597071 0.48878278 0.22524651]]

index 7

[[0.28622796 0.488645   0.22512704]]

index 8

[[0.28636017 0.48858171 0.22505812]]

index 9

[[0.28642834 0.48855152 0.22502014]]

index 10

[[0.28646357 0.4885367  0.22499973]]

index 11

[[0.28648179 0.48852929 0.22498892]]

index 12

[[0.28649123 0.48852554 0.22498323]]

index 13

[[0.28649612 0.48852362 0.22498026]]

index 14

[[0.28649865 0.48852263 0.22497872]]

index 15

[[0.28649996 0.48852212 0.22497791]]

index 16

[[0.28650064 0.48852186 0.22497749]]

index 17

[[0.286501   0.48852173 0.22497728]]

index 18

[[0.28650118 0.48852166 0.22497716]]

index 19

[[0.28650128 0.48852162 0.22497711]]

p=np.array([[0.65,0.28,0.07],[0.15,0.67,0.18],[0.12,0.36,0.52]])

#p2 = np.array([[0.21,0.68,0.11]])

p2 = np.array([[0.286, 0.489, 0.225]])

for i in range(20):

    print("index", i)

    p2 = np.dot(p2,p)

    print(p2)

index 0

[[0.28625 0.48871 0.22504]]

index 1

[[0.2863738 0.4886001 0.2250261]]

index 2

[[0.28643612 0.48855613 0.22500776]]

index 3

[[0.28646783 0.48853751 0.22499466]]

index 4

[[0.28648407 0.4885292  0.22498672]]

index 5

[[0.28649243 0.48852533 0.22498224]]

index 6

[[0.28649675 0.48852346 0.22497979]]

index 7

[[0.28649898 0.48852253 0.22497849]]

index 8

[[0.28650014 0.48852207 0.2249778 ]]

index 9

[[0.28650073 0.48852183 0.22497744]]

index 10

[[0.28650104 0.48852171 0.22497725]]

index 11

[[0.2865012  0.48852165 0.22497715]]

index 12

[[0.28650129 0.48852161 0.2249771 ]]

index 13

[[0.28650133 0.4885216  0.22497707]]

index 14

[[0.28650135 0.48852159 0.22497706]]

index 15

[[0.28650136 0.48852158 0.22497705]]

index 16

[[0.28650137 0.48852158 0.22497705]]

index 17

[[0.28650137 0.48852158 0.22497705]]

index 18

[[0.28650138 0.48852158 0.22497704]]

index 19

[[0.28650138 0.48852158 0.22497704]]

• Convergence: Whatever the state space is finite or infinite. Markov chain will be into a stationary distribution after many steps transition. And this stationary distribution is only associated with the transition matrix, not the intial state. Thus, Morkov chain has a feature of convergence. if initial state: X0 ∼ π0(x); state i: Xi ∼ πi(x), πi(x) = πi−1(x)P = π0(x)P^n. Once reaching stationary distribution, it has: Xn ∼ πn(x) = π(x); Xn+1 ∼ π(x); Xn+2 ∼ π(x). Namely: π(i)Pij = π(j)Pji for all i, j. So we call π(x) is the stationary distribution and Xn, Xn+1 and Xn+2 are the samples under stationary distribution. This feature is quite important and it is the basis of MCMC(Markov Chain Monte Carlo).

2.3. Sampling

Statistics and probability:

Figure 2.3.0 Statistics and probability

Probability, we also call prior information; statistics, also called posterior. In the real world (computer world), we only use statistics to evaluate theoritical model. That's why we need sampling to evaluate the probabilitic model. Using a finite number of randomly sampled points to compute a result is called sampling. The idea is simple. Generate enough points to get a representative sample of the problem, run the points through the system you are modeling, and then compute the results on the transformed points. 

For example, if we want to compute Pi: we can draw a square with side length 2 and a circle with radius 1 inside of the square. And we generate a set of uniformly distributed random points within the square and count how many fall inside the circle. The area of the circle is computed as the area of the square times the ratio of points inside the circle vs. the total number of points. Finally, we know that A=πr2, so we compute π=A/r2.

Fig 2.3.1 compute π

As for probability density function (PDF), the equation is: 

It also equals the area under the curve. It is easy to compute the integral with definite equation/formula. But for many curves, they are hard to analytically describe, not to mention integrate it like below:

Fig 2.3.2 Arbitrary curve

In this situation, we can use sampling methods to compute the integral. e.g. let x falls in [a,b], then building a box which wraps the curve [a,b]. Then generating a set of uniformly distributed random points within the box and count how many fall under the curve, and get the area under the curve. 

Then a question is How to generate samples under a distribution p(x)? This method is the so-called Monte Carlo sampling.

2.4. Monte Carlo Sampling

Monte Carlo sampling was invented by Stanley Ulam at Los Alamos National Laboratory to allow him to perform computations for nuclear reactions which were unsolvable on paper. we can use Monte Carlo to compute the probability density of any probability distribution.

There is an important sampling method called MCMC(Markov Chain Monte Carlo). As described before at section of Markov chain, we call π(x) is the stationary distribution and Xn, Xn+1 and Xn+2 are the samples under stationary distribution. One beautiful thought is set the stationary distribution as our target, p(x). Once the system entering into stationary distribution, all samples are satisfied to p(x). Then we can design the transition matrix Q for this Markov chain to make the samples generated satisfied to p(x).

Of course, this is just a brief description of the principle of MCMC. For more details you can refer to.

MCMC now becomes the most commonly used method to generate samples satisfied certain p(x). For example, in Numpy.random, there are gauss distribution, uniform distribution, and some other distributions. We can call these API for convenience. Besides, we also can use PyMC3.

3. Bayes Inference and Bayes Filter

3.1 Bayes Inference

Bayes Theorem is the basic framework of Bayes inference as shown in Equation 3, using prior information and likelihood to deduce posterior.  

In many applications, we need to fuse multi-source information to deduce the system status. Here is the formula to fuse multi-source information. We see the basic rule is under the Bayes Theorem framework, using the law of total probability to do factorization.

Equation 8. fusion of multi-source information

Here x is the system status, y.z are two measurements. we can view them as the measurement at different epochs. Assume z is the previous measurement and y is the current status. P(x|y,z) means the posterior probability of current status based on measurements y,z. p(y|x,z) means the conditional probability given the current status x and last measurement z. p(x|z) means the conditional probability of current status x given the measurement z. and p(y|z) means the conditional probability of current measurement given the last measurement.

Bayesian recursion formula:
We have introduced how to use Bayes Theorem to deduce system status. However, sometimes, we need to use the previous multi-status to infer. That's the Bayesian recursion formula.

Equation 9. Bayesian recursion formula

From Equation 9, Bayes recursion formula has the feature of Markov Chain. Use the conditional probability to make the transition between statuses.

Here is an example to practice Bayes Inference.

3.2 Bayes Filter

In practical, apart from the self-measurement, a system would be affected by a dynamic environment. For example, the system affects itself or outside action affects this system. We can build a scene like this. for a robot, it can move one step at each epoch. To get the accurate status of the system, we need to measure to evaluate system status. So there are two sections, section 1: the system itself can change from current status to next status.We also called it prection. Section 2: we can measure the real-time status of the system. The aim of the Bayes filter is to fuse the prediction and measurement to update the system status.

Assume u is the action (e.g. moving one step), x′ is the status before this action, x is the status after this action. So P(x|u,x′) means the posterior status after the action u. The form is:
(The effect of action towards status is displayed by the status transition model. here is an example.)

Equation 10. P(x|u,x′)

Then we have a framework for Bayes filter:

• Given the prior probability of system status, p(x)
• Given the system measurement z and action u at 1 to t: dt = {u1, z1,..., ut, zt}
• Given the measurement model/probability p(z|x)
• deduce the posterior probability p(x|u,x′). namely, Bel(xt)=P(xt|u1,z1…,ut,zt)
• Assumption 1: Markov Characteristic, namely,  The status at t is determined by the status at t−1 and action at t. The measurement at t is only related to the status at t. In other words, zt is the outer calibration of the system status, ut is the energy to predict system status.

Figure 3.2.1 Assumption 1

• Assumption 2: observation noisy (for zt) and model noisy (for xt) are independent.
• Assumption 3: Assume other environment factors unchanged.

So Bayes Filter is:

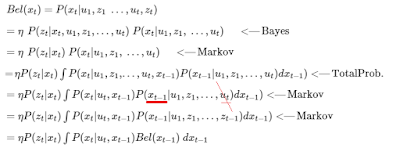Equation 11 (1)

Equation 11(2). Bayes Filter

We see Equation 11 (1), the first step is the expansion of Bayes Theorem. The inference of η is shown in Equation 11 (2). And step 2 is using the Markov characteristic, namely, zt is determined by xt. Step 3 is using the law of total probability to get xt-1. Step 4 is still the Markov feature, xt is determined by xt-1 and ut. Similarly, due to Markov feature, xt-1 is not related to ut.

In a nutshell, there are two steps: ∫P(xt|ut,xt−1)Bel(xt−1)dxt−1 is using xt-1 and ut to get the prediction status of xt. And ηP(zt|xt) is used to update the xt using zt.

Algorithm flow:

Figure 3.2.2 Algorithm flow

From this flow, we see there are two parts: update part and prediction part. When there is just an action (e.g. advancing one step, moving into next epoch), the system will be self-updated in a predicted manner. when doing a measurement, z, the system will fuse measurement, z, and prediction to update the status.

4. Practice: Bayes Filter

Here is an example to show how Bayes filter works.

• Assume a system has 10 different statuses. In the beginning, the probability of each status is equal. So the initial status of this system is belief = [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1].
• Assume there is no measurement. If the system moves into another status. then we need to make a prediction for system status. Currently, belief1 would equal belief. Of course, this is a special example, if the initial belief is [.35, .1, .2, .3, 0, 0, 0, 0, 0, .05]. That means, we think the system is more likely to be the first position. Then if the system moves on, the belief1 would be [.05, .35, .1, .2, .3, 0, 0, 0, 0, 0]. This process is a prediction.
• Then we have a list of possible measurement, hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0]). Where 1 means that position is a door. 0 means that position is a wall. Taking tracking a dog walking in a corridor as an example, one time of measurement may indicate it stops at a door or a wall. When z=1,=>door; z=0, =>wall. The initial probability for measurement should be: [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]. 
• Assume current measurement z equals 1 with a probability 75%. That means a 25% chance of wall. The probability for measurement should be p(z|x) = [0.3, 0.3, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.3, 0.1]. =likelihood
• Then the prior probability of this system is [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]. we have a measurement z = 1; then we can update the status by using p(x|z) = p(z|x)p(x)/normalization. so the posterior probability of status should be: [0.03, 0.03, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.03, 0.01]. As its sum doesn't equal 1, we need to normalization. So we let p(x|z)/sum(p(x|z)) = p(x|z)/0.16 = [0.1875, 0.1875, 0.0625, 0.0625, 0.0625, 0.0625, 0.0625, 0.0625, 0.1875, 0.0625].
• The source code is shown below:

def lh_hallway(hall, z, z_prob):

    """ compute likelihood that a measurement matches

    positions in the hallway."""

    

    try:

        scale = z_prob / (1. - z_prob)

    except ZeroDivisionError:

        scale = 1e8

    likelihood = np.ones(len(hall))

    likelihood[hall==z] *= scale

    return likelihood

def update(likelihood, prior):

    posterior = prior * likelihood

    return normalize(posterior)

def normalization(pdf)

    pdf /= sum(np.asarray(pdf, dtype=float))

    return pdf  

hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])

belief = np.array([0.1] * 10)

likelihood = lh_hallway(hallway, z=1, z_prob=.75)

posterior = update(likelihood, belief) 

posterior = normalization(posterior)

5. Conclusion

This post covered Bayes Theorem, Markov Chain, Monte Carlo, Bayes Inference and Bayes Filter. The link between those is:

Figure 5.1

We see, the framework of Bayes inference is to use likelihood and prior information to deduce the posterior. It is intuitive as sometimes we can't direct get the posterior information. We need to generate samples to approximate probabilities. The method we used is Monte Carlo. Actually, Monte Carlo means the way how to generate samples to approximate probabilities. This method is already applied in many random data applications. We may not know the principle of Monte Carlo, you need to know its function. 

And the framework of Bayes Filter includes two parts: one part is the prediction, one is the update. If there is no outer measurement, the transition of system status will be implemented by prediction. If there is a measurement, Bayes filter will combine prediction and measure to compute the posterior and update. 

Both Bayes Inference and Bayes Filter use the feature of Markov Chain, namely, the current status is only related to the last status.  

Bayes Filter is a kind of non-parametric filter as it doesn't directly evaluate the parameter. It uses a sampling method to approximate the posterior information. But these two parts (prediction and update) is the basis for other filters, e.g. Kalman filter, Extended Kalman filter. Particle filter and so on. Apart from Bayes Filter, Particle filter and Histogram filter are also non-parametric filters.

Kalman filter is a parametric filter as its probability is Gauss model. We only need to evaluate the mean and variance of the status to obtain the model. Then directly use this model to infer the transition of the system.

Reference

1. non-parametric filters: https://zhuanlan.zhihu.com/p/29025610
2. Bayes Filter: https://nbviewer.jupyter.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/02-Discrete-Bayes.ipynb
3. https://blog.csdn.net/liuyanpeng12333/article/details/81003340
4. https://blog.csdn.net/guoyunlei/article/details/80941375