[Research] Activation Functions

1. Introduction

In this post, I will show you some basic knowledge about the activation function in neural networks. Before our talk, you maybe want to ask some questions including why we need activation functions? what types of functions are there and what features they have? How to correctly choose the activation function in your practice? Then we will start our journey with these questions.

2. Meaning amd Features of activation functions

Activation functions for the hidden units are needed to introduce nonlinearity into the network. Without nonlinearity, hidden units would not make nets more powerful than just plain perceptrons (which do not have any hidden units, just input and output units). The reason is that a linear function of linear functions is again a linear function. However, it is the nonlinearity (i.e, the capability to represent nonlinear functions) that makes multilayer networks so powerful. Almost any nonlinear function does the job, except for polynomials. For backpropagation learning, the activation function must be differentiable, and it helps if the function is bounded; the sigmoidal functions such as logistic and tanh and the Gaussian function are the most common choices. Functions such as tanh or arctan that produce both positive and negative values tend to yield faster training than functions that produce only positive values such as logistic, because of better numerical conditioning.
An activation function generally has the following features:

• Non-linearity
• Differentiable
• Monotonicity
• f(x)≈x
• the range of the output 

3. Classification and Features

3.1 Sigmoid

Definition:
Sigmoid is also called Logistic activation function. It compresses the input within [0,1]. The equation of Sigmoid is:

Figure 3.1

its graph:

Figure 3.2

the graph of its derivative:

Figure 3.3

Feature:

• Advantages

The derivative of Sigmoid is: df(x)=f(x)(1-f(x)). This feature is very easy-to-use when computing the derivative.

• Disadvantages

a) gradient vanishing problem: From the figure 3.2, we can see when x is approaching 0 or 1, the graph becomes flat which means the derivative is approaching 0. In neural networks, those neurons whose outputs are approaching 0 or 1 are called saturated neurons. As we all know, the optimization process can speed up if the convergence speed is high. At this point, we need to let the output of neurons change significantly. But when x is big enough or small enough, the output f(x) almost has no change which leads to low convergence. The weights belonging to those saturated neurons will not update and the connected neurons' weights also update very slowly, which called gradient vanishing problem.

b) The output of Sigmoid is not zero-centred.
c) very high computational load.

3.2 Tanh

Definition:
Tanh is also called the hyperbolic tangent activation function. It compresses the input within [-1,1].

Figure 3.4

Figure 3.5

Figure 3.6

Feature:

• Disadvantages

a) The output of Sigmoid is zero-centred.
b) Tanh also faces the gradient vanishing problem as the Sigmoid does.

3.3 ReLU

Definition:
From the aforesaid, Sigmoid and Tanh both face the gradient vanishing problem. Therefore, we consider another nonlinear function, ReLU. It is also called rectified linear unit. Its equation is displayed in the form:

Figure 3.7

its graph:

Figure 3.8

the graph of its derivative:

Figure 3.9

Feature:

• Advantages

From the graph, when x>0, the output is x, so it does not saturate which means it is resistant to the gradient vanishing problem at least in the positive region.
When comparing the equation, ReLU is so simple that the computation is quite efficient.

• Disadvantages

a) The output of ReLU is not zero-centred.
b) The other issue with ReLU is that if x < 0 during the forward pass, the neuron remains inactive and it kills the gradient during the backward pass. Thus weights do not get updated, and the network does not learn. When x = 0 the slope is undefined at that point, but this problem is taken care of during implementation by picking either the left or the right gradient.

3.4 Leaky ReLU

To address the vanishing gradient issue in ReLU activation function when x < 0 we have something called Leaky ReLU which was an attempt to fix the dead ReLU problem. Its equation is shown below:

Figure 3.10

The concept of leaky ReLU is when x < 0, it will have a small positive slope of 0.1 (shown below).

Figure 3.11

This function somewhat eliminates the dying ReLU problem, but the results achieved with it are not consistent. Though it has all the characteristics of a ReLU activation function, i.e., computationally efficient, converges much faster, does not saturate in positive region.
The idea of leaky ReLU can be extended even further. Instead of multiplying x with a constant term we can multiply it with a hyperparameter which seems to work better the leaky ReLU. This extension to leaky ReLU is known as Parametric ReLU.

3.5 Parametric ReLU

The PReLU function is given by: 

Figure 3.12

Where α is a hyperparameter. The idea here was to introduce an arbitrary hyperparameter α, and this α can be learned since you can backpropagate into it. This gives the neurons the ability to choose what slope is best in the negative region, and with this ability, they can become a ReLU or a leaky ReLU.
In summary, it is better to use ReLU, but you can experiment with Leaky ReLU or Parametric ReLU to see if they give better results for your problem.

3.6 SWISH

It is also known as the self-gated activation function which is released by researchers at google. Mathematically it is represented as: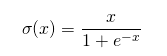

Figure 3.13

Figure 3.14

According to the paper, the SWISH activation function performs better than ReLU

From the above figure, we can observe that in the negative region of the x-axis the shape of the tail is different from the ReLU activation function and because of this the output from the Swish activation function may decrease even when the input value increases. Most activation functions are monotonic, i.e., their value never decreases as the input increases. Swish has one-sided boundedness property at zero, it is smooth and is non-monotonic. It will be interesting to see how well it performs by changing just one line of code.

Reference

https://jamesmccaffrey.wordpress.com/2017/07/06/neural-network-saturation/
https://www.learnopencv.com/understanding-activation-functions-in-deep-learning/
http://www.faqs.org/faqs/ai-faq/neural-nets/part2/section-10.html